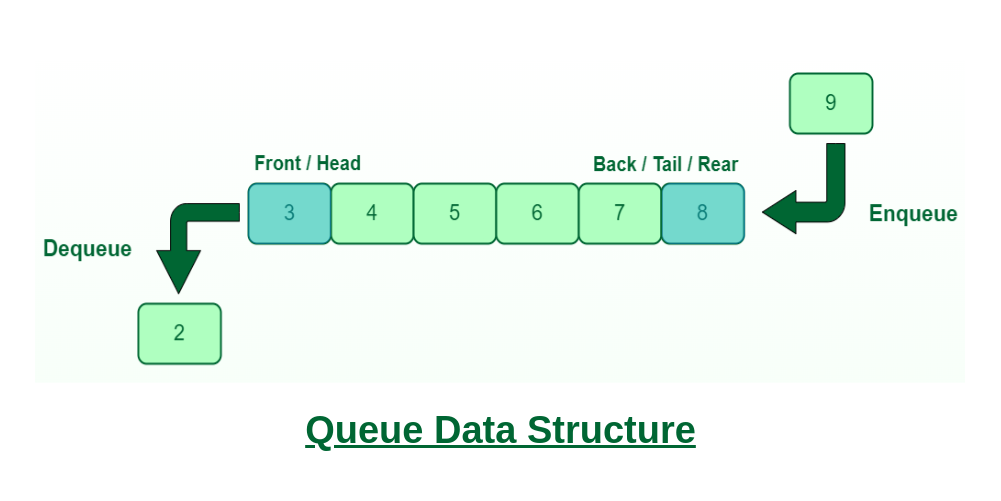
什么是队列数据结构? #
队列是一种线性数据结构。该数据结构遵循执行操作的特定顺序。顺序是先进先出( FIFO )。这意味着队列中最先插入的元素将最先出现,最后插入的元素将最后出现。它是一个有序列表,其中元素的插入是从一端(称为后端)完成的,元素的删除是从另一端(称为前端)完成的。与堆栈类似,可以对队列执行多个操作。当向队列中插入元素时,该操作称为“入队”;当从队列中删除元素时,该操作称为**“出队”。**
重要的是要知道,如果队列大小已满,我们无法插入元素,而当队列本身为空时,我们无法删除元素。如果我们尝试在队列已满后插入元素,则这种情况称为溢出,而如果我们尝试在队列为空后删除元素,则这种情况称为下溢。
我们将队列定义为一个列表,其中对列表的所有添加都在一端进行,而对列表的所有删除都在另一端进行。首先被推入订单的元素,首先对其执行操作。
队列的先进先出原理: #
- 队列就像等待买票的队伍,队列中的第一个人就是第一个得到服务的人。(即先到先得)。
- 队列中准备被服务的条目的位置,即将从队列中删除的第一个条目,称为队列的前端(有时称为队列****头),类似地,最后一个条目的位置队列中,即最近添加的队列,称为队列的后部(或**尾部)。见下图。
队列操作: #
-
**void enqueue(int Element):**执行此操作时,会在队列末尾(即后端)插入一个元素。(其中 T 是通用的,即我们可以定义任何类型的数据结构的队列。)此操作需要常数时间,即 O(1)。
-
int dequeue(): 执行该操作时,会从前端移除一个元素并返回。该操作需要常数时间,即 O(1)。
-
**Enqueue() ** –将一个元素添加(或存储)到队列末尾。其时间复杂度为O(1)。
-
**Dequeue() ** – 从队列中删除元素。其时间复杂度为O(1)。
-
**Peek() 或 front() ** -获取队列前端节点可用的数据元素,而不删除它。
-
**after() ** –此操作返回后端的元素而不删除它。
-
**isFull() ** –该操作指示队列是否为空。此操作也在 O(1) 内完成。
-
**isNull() ** –检查队列是否为空。
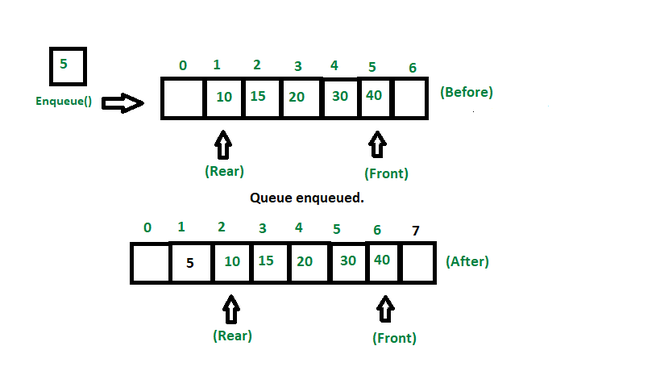
入队(): #
Queue 中的 Enqueue() 操作将一个元素添加(或存储)到队列末尾。 应采取以下步骤将数据排队(插入)到队列中:
- 步骤1:检查队列是否已满。
- 步骤2:如果队列已满,则返回溢出错误并退出。
- 步骤3:如果队列未满,则递增后指针以指向下一个空空间。
- 步骤 4:将数据元素添加到队列位置,即后部指向的位置。
- 步骤 5:返回成功。
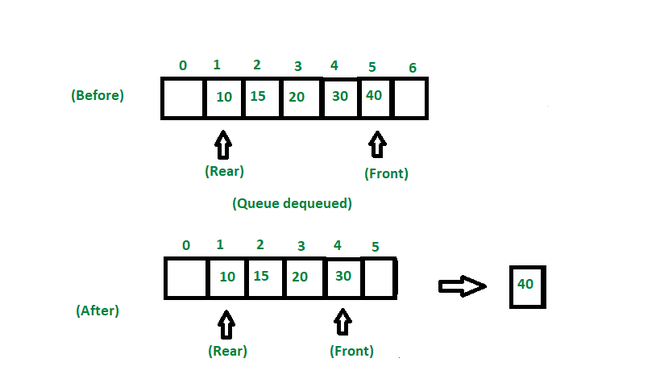
出队(): #
从队列中删除(或访问)第一个元素。执行出队操作的步骤如下:
- **步骤1:**检查队列是否为空。
- **步骤2:**如果队列为空,则返回下溢错误并退出。
- **步骤3:**如果队列不为空,则访问front指向的数据。
- **步骤 4:**增加前指针以指向下一个可用数据元素。
- **步骤 5:**返回成功。
dequeue(){
// removing element from the queue
// returns underflow when called
// on empty queue
if(this.isEmpty()){
document.write("<br>Queue is empty<br>");
return -1;
}
return this.items.shift();
}
// This code is contributed by Susobhan Akhuli
队列类型: #
- 简单队列:简单队列也称为线性队列,是队列的最基本版本。这里,插入元素即入队操作发生在队尾,移除元素即出队操作发生在队首。
- 循环队列: 在循环队列中,队列的元素充当圆环。循环队列的工作原理与线性队列类似,只是最后一个元素连接到第一个元素。它的优点是可以更好地利用内存。这是因为如果存在空白空间,即如果队列中的某个位置不存在元素,则可以轻松地在该位置添加元素。
- 优先级队列:该队列是一种特殊类型的队列。它的特点是它根据某种优先级排列队列中的元素。优先级可以是具有最高值的元素具有优先级,因此它创建一个按值降序排列的队列。优先级也可以是具有最低值的元素获得最高优先级,因此它依次创建一个值顺序递增的队列。
- 双端队列:顾名思义,双端队列意味着可以从队列的两端插入或删除元素,这与其他队列只能从一端插入或删除元素不同。由于此属性,它可能不遵守先进先出属性。
队列的实现: #
- **顺序分配:**队列可以使用数组来实现。它可以组织有限数量的元素。
- 链表分配: 队列可以使用链表来实现。它可以组织无限数量的元素。
队列的应用: #
- 多重编程:多重编程是指主存中同时运行多个程序。组织这些多个程序是至关重要的,并且这些多个程序被组织为队列。
- 网络:在网络中,队列用于路由器或交换机等设备。队列的另一个应用是邮件队列,它是存储数据和控制邮件消息文件的目录。
- 作业调度:计算机有一项任务来执行特定数量的作业,这些作业被安排一个接一个地执行。这些作业被一一分配给使用队列组织的处理器。
- 共享资源:队列用作单个共享资源的等待列表。
Queue的应用: #
- ATM 亭排队
- 售票柜台排队
- 键盘上的按键顺序
- CPU任务调度
- 每个客户在呼叫中心的等待时间。
队列的优点: #
- 可以轻松有效地管理大量数据。
- 由于遵循先进先出的规则,可以轻松执行插入和删除等操作。
- 当多个消费者使用特定服务时,队列非常有用。
- 队列对于数据进程间通信的速度很快。
- 队列可以用于其他数据结构的实现。
队列的缺点: #
- 从中间插入、删除元素等操作比较耗时。
- 空间有限。
- 在经典队列中,只有从队列中删除现有元素后才能插入新元素。
- 搜索元素需要 O(N) 时间。
- 必须事先定义队列的大小。
队列的数组表示: #
// Queue class
class Queue
{
// Array is used to implement a Queue
constructor()
{
this.items = [];
}
}
队列的链表表示: #
class QNode
{
constructor(key)
{
this.key = key;
this.next = null;
}
}
let front = ``null``, rear = ``null``;
不同类型的队列及其应用 #
介绍 : #
队列是一种线性结构 .遵循特定的操作执行顺序。顺序为先进先出 (FIFO)。队列的一个很好的例子是资源的任何消费者队列,其中先到达的消费者首先得到服务。在本文中,讨论了不同类型的队列。
队列类型: #
有五种不同类型的队列,用于不同的场景。他们是:
- 输入受限队列(这是一个简单队列)
- 输出受限队列(这也是一个简单队列)
- 循环队列
- 双端队列(Deque)
- 优先队列
- 优先级升序队列
- 优先级降序队列

1、循环队列: #
循环队列是一种线性数据结构,其操作基于 FIFO(先进先出)原则进行,最后一个位置连接回第一个位置以形成一个循环。它也被称为**“环形缓冲区”**。该队列主要用于以下情况:
- 内存管理:普通队列中未使用的内存位置可以在循环队列中利用。
- 交通系统:在计算机控制的交通系统中,采用循环队列,按照设定的时间一一重复地打开交通信号灯。
- CPU 调度:操作系统通常维护一个准备执行或等待特定事件发生的进程队列。
循环队列的时间复杂度为O(1)。
2、 输入受限队列: #
在这种类型的队列中,只能从一侧(后侧)输入,并且可以从两侧(前侧和后侧)删除元素。这种队列不遵循 FIFO(先进先出)。该队列用于以下情况:数据消耗需要按照 FIFO 顺序,但由于某种原因需要删除最近插入的数据,这种情况可能是不相关的数据、性能问题等。

输入限制队列的优点:
- 通过限制添加的项目数量来防止队列溢出和过载
- 帮助保持系统的稳定性和可预测的性能
输入限制队列的缺点:
- 如果限制设置得太低,可能会导致资源浪费并且物品经常被丢弃
- 如果限制设置得太高并且队列已满,可能会导致等待或阻塞,从而阻止添加新项目。
3.输出受限队列: #
在这种类型的队列中,可以从两侧(后侧和前侧)输入,并且只能从一侧(前侧)删除元素。该队列用于输入具有某种要执行的优先顺序并且输入甚至可以放置在第一位以便首先执行的情况。

**4.**双端队列: #
双端队列也是一种队列数据结构,其中插入和删除操作都在两端(前和后)进行。也就是说,我们可以在前后位置插入,也可以在前后位置删除。由于 Deque 同时支持堆栈和队列操作,因此它可以同时用作堆栈和队列操作。
Deque 数据结构支持 O(1) 时间内的顺时针和逆时针旋转,这在某些应用程序中非常有用。此外,使用双端队列可以有效解决需要删除和/或添加两端元素的问题。

双端队列
5. 优先级队列 : #
优先级队列是一种特殊类型的队列,其中每个元素都与一个优先级相关联,并根据其优先级提供服务。有两种类型的优先级队列。他们是:
-
**优先级升序队列:**可以任意插入元素,但只能删除最小的元素。
例如,假设有一个数组,其中元素 4、2、8 的顺序相同。所以,插入元素时,插入的顺序是相同的,而删除时,顺序是2、4、8。
-
**优先级降序队列:**可以任意插入元素,但只能首先从给定队列中删除最大的元素。
例如,假设有一个数组,其中元素 4、2、8 的顺序相同。所以,插入元素时,插入的顺序是相同的,而删除时,顺序是8、4、2。
优先级队列的时间复杂度为O(logn)。
6. 队列的应用: #
当事物不需要立即处理,但必须像广度优先搜索那样以先进先出的顺序处理时,就会使用队列。队列的这一属性使其在以下场景中也很有用。
- 当资源在多个消费者之间共享时。示例包括CPU 调度、磁盘调度。
- 当数据在两个进程之间异步传输时(数据接收速率不一定与发送速率相同)。示例包括 IO 缓冲区、管道、文件 IO 等。
- 线性队列:线性队列是一种将数据元素添加到队列末尾并从队列前面删除的队列。线性队列用于需要按照接收顺序处理数据元素的应用程序。示例包括打印机队列和消息队列。
- 循环队列:循环队列与线性队列类似,但队列尾部与队列前端相连。这可以有效利用内存空间并提高性能。循环队列用于需要以循环方式处理数据元素的应用程序。示例包括 CPU 调度和内存管理。
- 优先级队列:优先级队列是一种队列,其中每个元素都分配有一个优先级。具有较高优先级的元素在具有较低优先级的元素之前被处理。优先级队列用于需要以更高优先级处理某些任务或数据元素的应用程序。示例包括操作系统任务调度和网络数据包调度。
- 双端队列:双端队列也称为双端队列,是一种队列类型,可以从队列的任一端添加或删除元素。这使得数据处理更加灵活,并且可以用于需要在多个方向上处理元素的应用程序。示例包括作业调度和搜索算法。
- 并发队列:并发队列是一种队列,旨在处理同时访问队列的多个线程。并发队列用于多线程应用程序,其中需要以线程安全的方式在线程之间共享数据。示例包括数据库事务和 Web 服务器请求。
7. 队列问题: #
使用队列时可能出现的一些常见问题:
- 队列溢出:当队列达到其最大容量并且无法接受更多元素时,就会发生队列溢出。这可能会导致数据丢失并导致应用程序崩溃。
- 队列下溢:当尝试从空队列中删除元素时,就会发生队列下溢。这可能会导致错误和应用程序崩溃。
- 优先级反转:当低优先级任务占用高优先级任务所需的资源时,优先级队列中会发生优先级反转。这可能会导致处理延迟并影响系统性能。
- 死锁:当多个线程或进程互相等待对方释放资源时,就会出现死锁,导致所有线程都无法继续进行的情况。使用并发队列时可能会发生这种情况,并可能导致系统崩溃。
- 性能问题:队列性能可能会受到多种因素的影响,例如队列的大小、访问频率以及对队列执行的操作类型。队列性能不佳会导致系统性能变慢并降低用户体验。
- 同步问题:当多个线程同时访问同一队列时,可能会出现同步问题。这可能会导致数据损坏、竞争条件和其他错误。
- 内存管理问题:队列可能会消耗大量内存,尤其是在处理大型数据集时。可能会发生内存泄漏和其他内存管理问题,从而导致系统崩溃和其他错误。