矩阵数据结构
#

矩阵表示按行和列的顺序排列的数字的集合。必须将矩阵的元素括在圆括号或方括号中。 例如：

具有 9 个元素的矩阵如下所示。

该矩阵M有 3 行和 3 列。矩阵M的每个元素都可以通过其行号和列号来引用。例如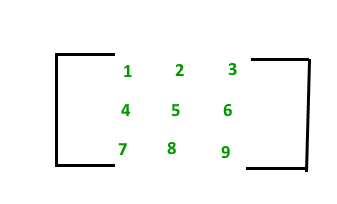，M[2][3] = 6。

矩阵是由行和列组成的二维数组。它是条目水平或垂直行中元素的排列。

矩阵或网格的声明
#

声明矩阵或二维数组的语法与一维数组的语法非常相似，如下所示。

int arr[行数][列数];

但是，它会生成如下所示的数据结构：

矩阵的表示

从上图中可以看出，元素按行和列进行组织。如上图所示，单元格 x[0][0] 是第一行第一列的第一个元素。第一个方括号内的值表示行号，第二个方括号内的值表示列号。（即 x[行][列]）。

初始化矩阵或网格
#

初始化二维数组有两种方法。

方法一

int arr[4][3]={1, 2, 3, 4, 5, 6, 20, 80, 90, 100, 110, 120};

方法2

int arr[4][3]={{1, 2, 3}, {4, 5, 6}, {20, 80, 90}, {100, 110, 120}};

以下是在声明期间初始化元素的两种方法。这里，首选第二种方法，因为第二种方法更具可读性和理解性，以便您可以直观地看到arr[][] 由四行三列组成。

如何访问矩阵或网格中的数据
#

与一维数组一样，可以通过使用矩阵的索引来访问各个元素来随机访问矩阵。单元格有两个索引，一个为其行号，另一个为其列号。我们可以使用X[i][j]来访问矩阵第 i行 第 j列的元素。

从矩阵中访问第 i行第 j列元素的语法：

int 值 = X[i][j];

如何打印矩阵或网格的元素：
#

可以使用两个“for”循环来打印矩阵或二维数组的元素。

//上述方法的 JS 代码
let arr = [[1, 2, 3, 4],
		[5, 6, 7, 8],
		[9, 10, 11, 12]];
for (let i = 0; i < 3; i++) {
let s="";
	for (let j = 0; j < 4; j++) {
		s+=(arr[i][j]+" ");
	}
	console.log(s);
}

1.在矩阵中搜索：
#

给定一个大小为 N x M 的矩阵 mat[][]，其中每行和每列都按升序排序，并给出数字 X。任务是确定元素 X 是否存在于矩阵中。

例子：

输入： mat[][] = { {1, 5, 9}, {14, 20, 21}, {30, 34, 43} } x = 14 输出： YES

输入： mat[][] = { {1, 5, 9, 11}, {14, 20, 21, 26}, {30, 34, 43, 50} } x = 42 输出： NO

解决方案：

有很多方法可以解决这个问题，但我们在这里讨论一种非常幼稚或暴力的方法。

一个简单的解决方案是将x与矩阵的每个元素进行一一比较。如果匹配，则返回 true。如果我们到达末尾则返回 false。该解法的时间复杂度为O(nxm)。

<script>
	function searchInMatrix(arr, x) {
		let m = arr.length, n = arr[0].length;

		for (let i = 0; i < m; i++) {
			for (let j = 0; j < n; j++) {
				if (arr[i][j] == x)
					return true;
			}
		}
		return false;
	}

// 驱动程序测试上述内容

	let x = 8;
	let arr
		= [[0, 6, 8, 9, 11],
		[20, 22, 28, 29, 31],
		[36, 38, 50, 61, 63],
		[64, 66, 100, 122, 128]];

	if (searchInMatrix(arr, x))
		document.write("YES" + "<br>");
	else
		document.write("NO" + "<br>");
</script>

时间复杂度： O(M*N)，其中M和N分别是行数和列数。 辅助空间： O(1)

2.打印矩阵对角线的程序
#

给定一个二维方阵，打印主对角线和次对角线。

例子：

输入： 1 2 3 4 4 3 2 1 7 8 9 6 6 5 4 3 输出： 主对角线：1, 3, 9, 3 次对角线：4, 2, 8, 6

输入： 1 1 1 1 1 1 1 1 1 输出： 主对角线：1, 1, 1 次对角线：1, 1, 1

解决方案：

主对角线由元素 A00、A11、A22、A33 形成。主对角线的条件：行列条件是行=列。

次对角线由元素 A03、A12、A21、A30 形成。次对角线的条件：行列条件为行 = numberOfRows – 列 -1。

//打印主对角线的函数
function printPrincipalDiagonal(mat, n)
{
	let s = "";
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {

			// Condition for principal diagonal
			if (i == j)
			{
				s += mat[i][j];
				s += " ";
			}
		}
	}
	console.log("Principal Diagonal: "+s);
	
}

//打印次要对角线的函数
function printSecondaryDiagonal(mat,n)
{
	let s="";
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {

			// Condition for secondary diagonal
			if ((i + j) == (n - 1))
			{
				s += mat[i][j];
				s +=" ";
			}
		}
	}
	console.log("Secondary Diagonal: "+s);
}

let n = 4;
let a = [[ 1, 2, 3, 4 ],
    [ 5, 6, 7, 8 ],
    [ 1, 2, 3, 4 ],
    [ 5, 6, 7, 8 ] ];

printPrincipalDiagonal(a, n);
printSecondaryDiagonal(a, n);

时间复杂度： O(n2)，由于涉及嵌套循环，所以时间复杂度是平方。 辅助空间： O(1)。

3. 对给定矩阵进行排序：
#

给定 anxn 矩阵。问题是按照严格的顺序对给定的矩阵进行排序。这里严格顺序意味着矩阵的排序方式使得一行中的所有元素都按升序排序，对于行“i”，其中 1 <= i <= n-1，行“i”的第一个元素大于或等于行“i-1”的最后一个元素。

例子：

输入： mat[][] = { {5, 4, 7}, {1, 3, 8}, {2, 9, 6} } 输出： 1 2 3 4 5 6 7 8 9

解决方案：

解决这个问题的想法是创建一个大小为 n^2 的 temp[] 数组。从第一行开始，将给定矩阵的元素逐一复制到 temp[] 中。对温度[]进行排序。现在将 temp[] 的元素一一复制回给定的矩阵。

// JS 实现对给定的矩阵//函数进行排序，以对给定的矩阵进行排序
function sortMat(mat, n)
{

// 大小为 n ^ 2的//临时矩阵
	let temp = [];
	let k = 0;
	
// 逐个复制矩阵元素
	// leto temp[]
	for (let i = 0; i < n; i++)
		for (let j = 0; j < n; j++)
			temp[k++] = mat[i][j];
			
	// sort temp[]
	temp.sort(function (a, b) { return b - a });
	
	// 逐个复制 temp[] 中的元素
	// in mat[][]
	k = 0;
	for (let i = 0; i < n; i++)
		for (let j = 0; j < n; j++)
			mat[i][j] = temp[k++];
}

// 打印给定矩阵的函数
function printMat(mat, n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++)
			console.log(mat[i][j]);
	}
}

// 驱动程序测试上述内容
let mat = [[5, 4, 7], [1, 3, 8], [2, 9, 6]];
let n = 3;
printMat(mat, n);
sortMat(mat, n);
printMat(mat, n);

时间复杂度： O(n2log2n)。 辅助空间： O(n2)，因为已占用 n * n 额外空间。

4. 将矩阵旋转 180 度
#

给定一个方阵，任务是在不使用任何额外空间的情况下将其逆时针方向旋转 180 度。

例子：

输入：

1 2 3 4 5 6 7 8 9 输出：

9 8 7 6 5 4 3 2 1

输入：

1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 输出：

6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1

解决方案：

解决此问题需要四个步骤： 1- 求矩阵的转置。 2- 反转转置的列。 3-求矩阵的转置。 4- 转置的反转列

分析：

设给定矩阵为 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

首先我们找到转置。 1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16

然后我们反转每列的元素。 4 8 12 16 3 7 11 15 2 6 10 14 1 5 9 13

然后再次转置 4 3 2 1 8 7 6 5 12 11 10 9 16 15 14 13

然后我们再次反转每列的元素 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1

// 将矩阵向左旋转 180 的 Javascript 程序
let R= 4
let C= 4

// 将矩阵旋转 180 度的函数
function reverseColumns(arr)
{
	for (let i = 0; i < C; i++)
		for (let j = 0, k = C - 1; j < k; j++, k--)
			{
			let x= arr[j][i];
			arr[j][i] = arr[k][i];
			arr[k][i]=x;
			}
			
}

// 矩阵转置函数
function transpose(arr)
{
	for (let i = 0; i < R; i++)
		for (let j = i; j < C; j++)
			{
			let x= arr[j][i];
			arr[j][i] = arr[i][j];
			arr[i][j]=x;
		}
}

// 显示矩阵的函数
function printMatrix(arr)
{
	console.log(arr);
}

// 逆时针旋转矩阵的函数
// 旋转 180 度
function rotate180(arr)
{
	transpose(arr);
	reverseColumns(arr);
	transpose(arr);
	reverseColumns(arr);
}
let arr = [[1, 2, 3, 4 ],
        [ 5, 6, 7, 8 ],
        [ 9, 10, 11, 12 ],
        [ 13, 14, 15, 16 ]];
rotate180(arr);
printMatrix(arr);

时间复杂度： O(R*C) 辅助空间： O(1)

5.查找矩阵中的唯一元素
#

给定一个具有 n 行和 m 列的矩阵 mat[][]。我们需要找到矩阵中唯一的元素，即矩阵中不重复的元素或频率为1的元素。

例子：

输入：

20 15 30 2 2 3 5 30 6 7 6 8 输出： 3 20 5 7 8 15

输入：

1 2 3
5 6 2 1 3 5 6 2 2 **输出：**矩阵中没有唯一元素

解决方案：

这个想法是使用散列并遍历矩阵的所有元素，如果字典中存在某个元素，则增加其计数。否则插入一个值为 1 的元素。

// JS code

let mat = [[1, 2, 3, 20], [5, 6, 20, 25], [1, 3, 5, 6], [6, 7, 8, 15]];

let max = 0;
let flag = 0;
for (let i = 0; i < mat.length; i++) {
for (let j = 0; j < mat.length; j++) {
	if (max < mat[i][j]) {
	max = mat[i][j];
	}
}
}

let b = new Array(max + 1).fill(0);
for (let i = 0; i < mat.length; i++) {
for (let j = 0; j < mat.length; j++) {
	let y = mat[i][j];
	b[y]++;
}
}

for (let i = 1; i <= max; i++) {
if (b[i] == 1) {
	console.log(i + " ");
	flag = 1;
}
}

if (!flag) {
console.log("No unique element in the matrix");
}

时间复杂度： O(m*n)，其中 m 是行数，n 是列数。 辅助空间： O(max(矩阵))。

矩阵和行列式的应用
#

矩阵和行列式的一种应用是它可以用来求解两个或三个变量的线性方程。矩阵和行列式还用于检查任何系统的一致性，无论它们是否一致。

使用矩阵的逆矩阵求解线性方程组
#

线性方程组的解可以通过矩阵的逆来求得。设方程为：

a ₁ x + b ₁ y + c ₁ z = d ₁

a ₂ x + b ₂ y + c ₂ z = d ₂

a ₃ x + b ₃ y + c ₃ z = d ₃

这些方程可以使用矩阵表示如下

\begin{bmatrix} a_{1}x +b_{1}y+c_{1}z\ a_{2}x +b_{2}y+c_{2}z \ a_{3}x +b_ {3}y+c_{3}z \end{bmatrix}= \begin{bmatrix} d_{1}\ d_{2}\ d_{3} \end{bmatrix}

进一步这可以写成

\begin{bmatrix} a_{1} & b_{1} &c_{1} \ a_{2}& b_{2} & c_{2}\ a_{3} & b_{3} & c_{3} \end{bmatrix} \begin{bmatrix} x \ y\ z \end{bmatrix}= \begin{bmatrix} d_{1} \ d_{2}\ d_{3} \end{bmatrix}

进一步这个系统可以写成 AX=B

其中矩阵 A 包含未知变量的系数。

\begin{bmatrix} a_{1} & b_{1} &c_{1} \ a_{2}& b_{2} & c_{2}\ a_{3} & b_{3} & c_{3} \end{b矩阵}

矩阵 X 是包含未知变量的列矩阵。

X =

矩阵B也是一个列矩阵，它包含常数。

\begin{bmatrix} d_{1} \ d_{2}\ d_{3} \end{bmatrix}

因此，如上所述，线性方程组可以转换为矩阵的形式，可以写为：

AX=B

如果 A 是非奇异矩阵，则 A -1存在。

两边都乘以 A -1

(A -1) * AX = (A -1) * B

IX = (A -1) * B

X = (A -1) * B

这为未知变量提供了唯一的解决方案。该解决方案将是唯一的，因为任何非奇异矩阵都有唯一的逆矩阵。

如果 A 是奇异矩阵，则 A -1不存在。在这种情况下|A| = 0，所以你必须计算 (adj A)B。

如果 (adj A)B ≠ O，则线性方程组不存在任何一个，并且该系统将不一致。
如果 (adj A)B = O，则线性方程组将具有零解或无穷多个解，这就是为什么如果系统没有任何解，则系统可能会不一致，如果有无穷多个解，则系统可能会一致解决方案。

系统的一致性
#

根据方程组拥有的解的数量，可以认为方程组是一致的或不一致的。

**一致系统：**如果方程组有解，则称该方程组是一致的。
**不一致系统：**如果一个方程组没有解，则称该方程组是不一致的。

示例问题
#

问题 1. 使用矩阵求解以下线性方程

2x + y = 3

2x + 3y = 6

解决方案：

上述线性方程组可以写成 AX = B 的形式，其中 A 是系数矩阵，X 是未知变量矩阵，B 是常数矩阵。

A=
$\begin{bmatrix} 2 &1 \ 2 &3 \end{bmatrix}$

X =
$\begin{bmatrix} x \ y \end{bmatrix}$

B=
$\begin{bmatrix} 3 \ 6 \end{bmatrix}$

首先找出|A|

如你所见|A| = 4 ≠ 0。因此，方程组是一致的并且将具有唯一解，并且可以使用 X = A -1 B找到解

$A^{-1} = \frac{adj A}{|A|}$

一个-1 =
$\frac{1}{4}\begin{bmatrix} 3 &-1 \ -2 &2 \end{bmatrix}$

X = A -1 B

$\begin{bmatrix} x \ y \end{bmatrix}$
=
$\frac{1}{4}\begin{bmatrix} 3 &-1 \ -2 &2 \end{bmatrix} \begin{bmatrix} 3 \ 6 \end{bmatrix}$

$\begin{bmatrix} x \ y \end{bmatrix}$
=
$\frac{1}{4} \begin{bmatrix} 9-6 \ -6+12 \end{bmatrix}$

$\begin{bmatrix} x \ y \end{bmatrix}$
=
$\frac{1}{4} \begin{bmatrix} 3 \ 6 \end{bmatrix}$

从这里你可以得出结论

x = 3/4

y = 6/4

问题2. 说出给定系统是否一致

x + 3y = 5

2x + 6y = 8

解决方案：

上述方程组可以写成AX=B的形式，其中

A=
$\begin{bmatrix} 1 & 3\ 2 & 6 \end{bmatrix}$

X =
$\begin{bmatrix} x \ y \end{bmatrix}$

B=
$\begin{bmatrix} 5 \ 8 \end{bmatrix}$

现在检查 A 的行列式

|一个| = 6 – 6 = 0克

为了检查系统的一致性，你必须检查 (adj A)B

形容词 A =
$\begin{bmatrix} 6 & -3\ -2 & 1 \end{bmatrix}$

(形容词 A)B =
$\begin{bmatrix} 6 & -3\ -2 & 1 \end{bmatrix} \begin{bmatrix} 5 \ 8 \end{bmatrix}$

(形容词 A)B =
$\begin{bmatrix} 30-24 \ -10+8 \end{bmatrix}$

(形容词 A)B =
$\begin{bmatrix} 6 \ -2 \end{bmatrix}$

由于 (adj A)B ≠ 0，因此给定线性方程组的解不存在。因此，方程组是不一致的。

问题 3. 使用矩阵法求解线性方程组

x – y + 2z = 7

3x + 4y – 5z = -5

2x – y + 3z = 12

解决方案：

上述方程组可以写成AX=B的形式，其中

A=
$\begin{bmatrix} 1 & -1 &2 \ 3& 4 &-5 \ 2& -1 & 3 \end{bmatrix}$

X =
$\begin{bmatrix} x \ y \ z \end{bmatrix}$

B=
$\begin{bmatrix} 7 \ -5 \ 12 \end{bmatrix}$

现在检查 A 的行列式

|一个| = 1 * (12 – 5) + 1 * (9 + 10) + 2 * (-3 – 8)

|一个| = 7 + 19 – 22 = 4

|一个| ≠0

因此，它的逆存在，因此存在唯一解，可以通过 X = A -1 B找到

$A^{-1} = \frac{adj A}{|A|}$

一个-1 =
$\frac{1}{4}\begin{bmatrix} 7 & 1 &-3 \ -19& -1 &11\ -11& -1 & 7 \end{bmatrix}$

X = A -1 B

$\begin{bmatrix} x \ y \ z \end{bmatrix}$
=
$\frac{1}{4}\begin{bmatrix} 7 & 1 &-3 \ -19& -1 &11\ -11& -1 & 7 \end{bmatrix} \begin{bmatrix} 7 \ -5 \ \ 12 \end{b矩阵}$

$\begin{bmatrix} x \ y \ z \end{bmatrix}$
=
$\frac{1}{4} \begin{bmatrix} 49-5-36 \ -133+5+132 \ -77+5+84 \end{bmatrix}$

$\begin{bmatrix} x \ y \ z \end{bmatrix}$
=
$\frac{1}{4}\begin{bmatrix} 8 \ 4 \ 12 \end{bmatrix}$

$\begin{bmatrix} x \ y \ z \end{bmatrix}$
=
$\begin{bmatrix} 2 \ 1 \ 3 \end{bmatrix}$

从这里，您可以看到 x = 2、y = 1 和 z = 3。

因此，x = 2、y = 1、z = 3。