堆数据结构
#

什么是堆数据结构？
#

堆是一种特殊的基于树的数据结构，其中树是完全二叉树。

堆的类型：
#

一般来说，堆有两种类型。

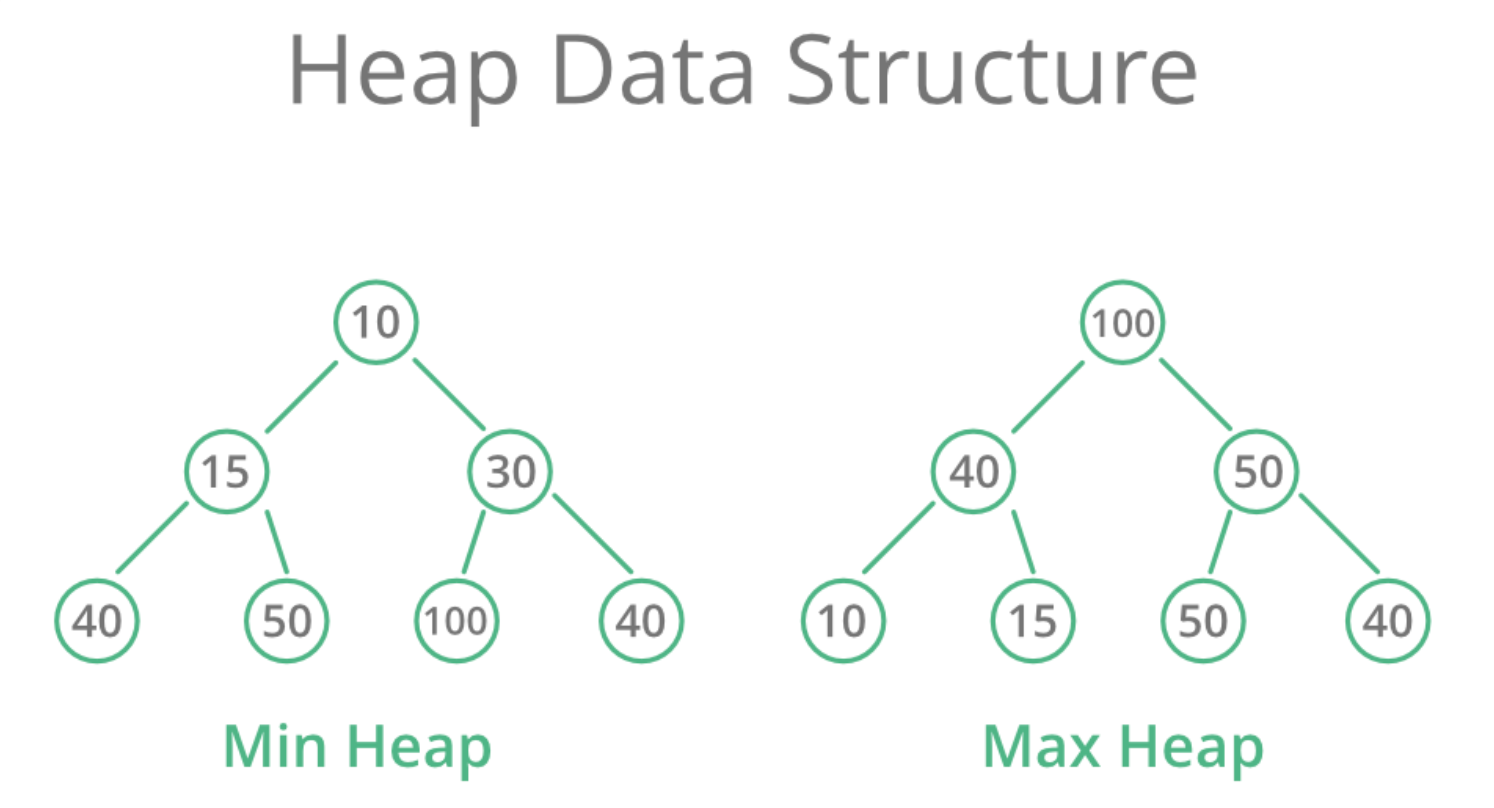
最大堆：
#

在这个堆中，根节点的值必须是其所有子节点中最大的，并且其左右子树也必须执行相同的操作。最大堆中所需的比较总数取决于树的高度。完全二叉树的高度始终为logn；因此，时间复杂度也是 O(logn)。

最小堆：
#

在这个堆中，根节点的值必须是其所有子节点中最小的，并且其左右子树也必须执行相同的操作。

最小堆中所需的比较总数取决于树的高度。完全二叉树的高度始终为logn；因此，时间复杂度也是 O(logn)。

堆的属性：
#

堆具有以下属性：
#

**完全二叉树：**堆树是完全二叉树，这意味着树的所有级别都已完全填充，除了最后一层（可能是从左到右填充）之外。此属性确保使用数组有效地表示树。
**堆属性：**该属性确保根据堆类型，最小（或最大）元素始终位于树的根部。
父子关系：索引i处的父节点与其子节点之间的关系由以下公式给出：对于从 0 开始的节点编号索引，左子节点位于索引2i+1，右子节点位于索引2i+2。
**高效的插入和删除：**堆树中的插入和删除操作是高效的。新元素将插入到最右下层的下一个可用位置，并通过将元素与其父元素进行比较并在必要时进行交换来恢复堆属性。删除根元素涉及用最后一个元素替换它并向下堆放。
**高效访问极值元素：**最小或最大元素始终位于堆的根部，允许恒定时间访问。

堆支持的操作：
#

min-heap和max-heap支持的操作是相同的。区别只是 min-heap 在树的根部包含最小元素，而 max-heap 在树的根部包含最大元素。

堆化：
#

它是重新排列元素以保持堆数据结构属性的过程。当某个节点由于该节点上的某些操作而在堆中造成不平衡时，就会执行此操作。平衡树需要O(log N) 。

对于**最大堆，**它以最大元素是二叉树的根的方式进行平衡。
对于**最小堆，**它以最小元素是二叉树的根的方式进行平衡。

插入：
#

如果我们向堆中插入一个新元素，因为我们向堆中添加一个新元素，那么它会扭曲堆的属性，所以我们需要执行heapify操作，以便它保持堆的属性。

此操作也需要**O(logN)**时间。

例子：

假设初始堆（取max-heap）如下

8 /
4 5 /
1 2

现在如果我们将 10 插入堆中 8 /
4 5 / \ / 1 2 10

heapify 操作后最终堆将如下所示 10 /
4 8 / \ / 1 2 5

删除：
#

如果我们从堆中删除元素，它总是删除树的根元素并将其替换为树的最后一个元素。
由于我们从堆中删除根元素，它会扭曲堆的属性，因此我们需要执行heapify操作，以便它保持堆的属性。

需要**O(logN)**时间。

例子：

假设初始堆（取最大堆）如下 15 /
5 7 /
2 3

现在，如果我们将堆中 15 删除，它将临时被树的叶节点替换。 3 /
5 7 /
2

heapify 操作后最终堆将如下所示 7 /
5 3 /
2

getMax（对于最大堆）或 getMin（对于最小堆）：
#

它分别找到max-heap和min-heap的最大元素或最小元素，并且我们知道最小和最大元素将始终分别是 min-heap 和 max-heap 的根节点本身。需要 O(1) 时间。

删除最大或删除最小：
#

此操作分别返回并删除最大堆和最小堆中的最大元素和最小元素。也就是删除的是堆二叉树的根元素。

堆数据结构的实现：
#

以下代码是max-heap的实现。

maxHeapify是负责恢复Max Heap属性的函数。它相应地排列节点i及其子树，以便维护堆属性。

假设我们有一个数组，arr[]代表完整的二叉树。第 i个节点的左子节点和右子节点位于索引2*i+1和2*i+2中。
我们将当前元素的索引i设置为“MAXIMUM”。
如果arr[2 * i + 1] > arr[i]，即左孩子大于当前值，则将其设置为“MAXIMUM”。
类似地，如果arr[2 * i + 2] > arr[i]，即右子节点大于当前值，则将其设置为“MAXIMUM”。
将“MAXIMUM”与当前元素交换。
重复步骤**2到5，**直到堆的属性恢复。

JavaScript 代码示例：

class MaxHeap {
  constructor(maxSize) {
    // 初始化堆中的数组
    this.arr = new Array(maxSize).fill(null);

    // 设置最大堆的大小
    this.maxSize = maxSize;

    // 设置堆中元素的大小
    this.heapSize = 0;
  }

  // 以给定的索引作为根节点，对子树进行堆化。
  MaxHeapify(i) {
    const l = this.lChild(i);
    const r = this.rChild(i);
    let largest = i;
    if (l < this.heapSize && this.arr[l] > this.arr[i]) {
      largest = l;
    }
    if (r < this.heapSize && this.arr[r] > this.arr[largest]) {
      largest = r;
    }
    if (largest !== i) {
      const temp = this.arr[i];
      this.arr[i] = this.arr[largest];
      this.arr[largest] = temp;
      this.MaxHeapify(largest);
    }
  }

  // 返回第i个索引元素的父级索引。
  parent(i) {
    return Math.floor((i - 1) / 2);
  }

  // 返回左侧子代的索引。
  lChild(i) {
    return 2 * i + 1;
  }

  // 返回右子节点的索引。
  rChild(i) {
    return 2 * i + 2;
  }

  // 删除根元素中包含最大元素。
  removeMax() {
    // 检测对数组是否为空
    if (this.heapSize <= 0) {
      return null;
    }
    if (this.heapSize === 1) {
      this.heapSize -= 1;
      return this.arr[0];
    }

    // 移除最大元素
    const root = this.arr[0];
    this.arr[0] = this.arr[this.heapSize - 1];
    this.heapSize -= 1;

    // 回复最大堆的属性
    this.MaxHeapify(0);

    return root;
  }

  // 在第 i 个元素插入新值
  increaseKey(i, newVal) {
    this.arr[i] = newVal;
    while (i !== 0 && this.arr[this.parent(i)] < this.arr[i]) {
      const temp = this.arr[i];
      this.arr[i] = this.arr[this.parent(i)];
      this.arr[this.parent(i)] = temp;
      i = this.parent(i);
    }
  }
  //   获取堆的最大元素
  getMax() {
    return this.arr[0];
  }
  // 获取堆的大小
  curSize() {
    return this.heapSize;
  }

  // 从指定索引删除元素
  deleteKey(i) {
    // 它将键值
    // 增加到无穷大，然后删除
    // 最大值。
    this.increaseKey(i, Infinity);
    this.removeMax();
  }

  // 在大堆中插入元素
  insertKey(x) {
    // 检车元素是否可以插入到堆中
    if (this.heapSize === this.maxSize) {
      console.log("\n 不能插入堆中 \n");
      return;
    }

    let i = this.heapSize;
    this.arr[i] = x;

    // 插入元素到堆的尾部
    this.heapSize += 1;

    // 检查最大堆属性
    // 如果违反，则恢复它.
    while (i !== 0 && this.arr[this.parent(i)] < this.arr[i]) {
      const temp = this.arr[i];
      this.arr[i] = this.arr[this.parent(i)];
      this.arr[this.parent(i)] = temp;
      i = this.parent(i);
    }
  }
}

// 测试上述功能的驱动程序。
// 假设堆的最大大小为15。
const h = new MaxHeap(15);
// 输入数值
console.log("Entered 6 keys: 3, 10, 12, 8, 2, 14 \n");

h.insertKey(3);
console.log(h.arr)
h.insertKey(10);
console.log(h.arr);
h.insertKey(12);
console.log(h.arr)
h.insertKey(8);
console.log(h.arr);
h.insertKey(2);
console.log(h.arr);
h.insertKey(14);
console.log(h.arr);

// 打印堆的当前大小。
console.log("打印堆的当前大小" + h.curSize() + "\n");

// 打印根元素 实际上是最大的元素。
console.log("根元素" + h.getMax() + "\n");

// 删除索引2的键。
h.deleteKey(2);

// 删除后，打印堆的大小
console.log("当前堆的大小是：" + h.curSize() + "\n");

// 在堆中插入 15 和 5 两个数字
h.insertKey(15);
h.insertKey(5);

console.log("当前堆的大小是： " + h.curSize() + "\n");

console.log("当前堆中最大的元素是： " + h.getMax() + "\n");

堆数据结构的应用：
#

优先级队列： 优先级队列可以使用二叉堆高效地实现，因为它支持**O(log N)**时间内的 insert()、delete() 和 extractmax()、decreaseKey() 操作。
二项式堆和斐波那契堆是二项式堆的变体。这些变体也在**O(log N)**时间内执行联合，这是二叉堆中的 O(N) 操作。
**顺序统计：**堆数据结构可用于有效地查找数组中第 k 个最小（或最大）元素。你可以看这篇 gfg文章来了解更多关于第 k 个最小或最大元素的信息。