图数据结构与算法 #
介绍: #
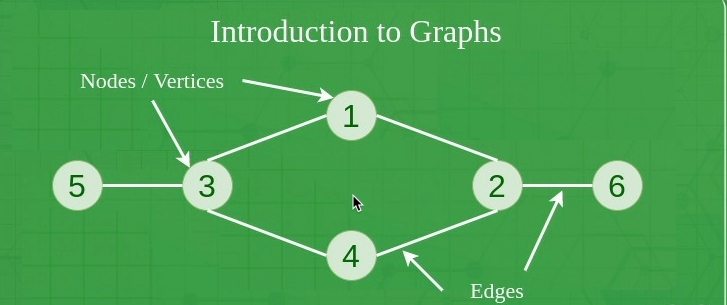
图是由顶点和边组成的非线性数据结构。顶点有时也称为节点,边是连接图中任意两个节点的线或弧。更正式地说,图由一组顶点(V)和一组边(E )组成。**该图用G(V, E)**表示。
图数据结构是表示和分析对象或实体之间复杂关系的强大工具。它们在社交网络分析、推荐系统和计算机网络等领域特别有用。在体育数据科学领域,图数据结构可用于分析和理解球队表现和场上球员互动的动态。
将一场足球比赛想象成一个连接网络,其中球员是节点,他们在场上的互动是边缘。这种连接网络正是图数据结构所代表的,它是洞察体育运动中团队表现和运动员动态的关键。
图的组成部分 #
- **顶点:**顶点是图的基本单位。有时,顶点也称为顶点或节点。每个节点/顶点都可以被标记或未标记。
- **边:**绘制或使用边来连接图的两个节点。它可以是有向图中的有序节点对。边可以以任何可能的方式连接任意两个节点。没有规则。有时,边也称为弧。每条边都可以标记/未标记。
图表类型 #
1. 空图 #
如果图中没有边,则该图称为空图。
2. 简单图 #
仅具有单个顶点的图,它也是可能的最小图。
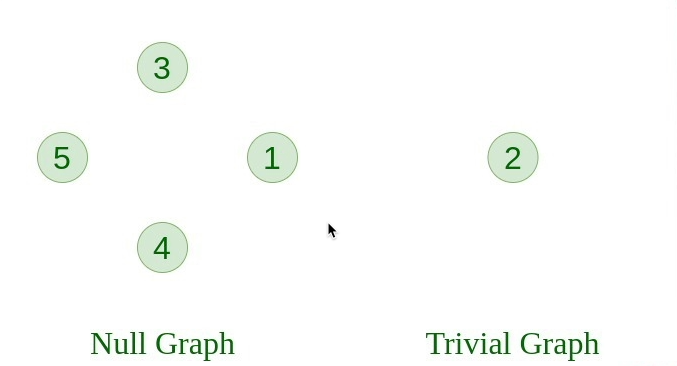
3.无向图 #
边没有任何方向的图。也就是说,在每条边的定义中,节点都是无序对。
4. 有向图 #
边有方向的图。也就是说,节点在每条边的定义中都是有序对的。
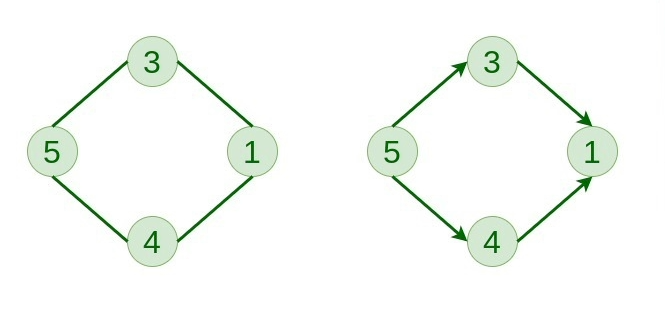
5.连通图 #
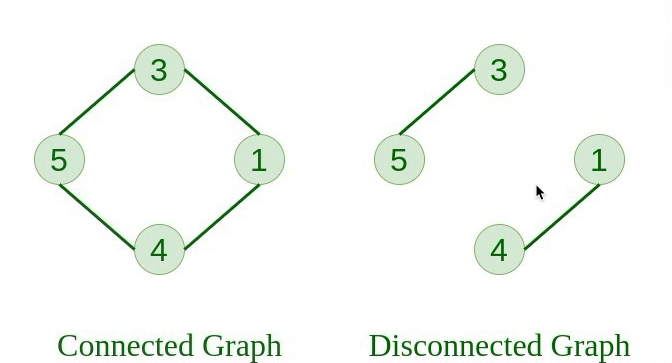
从一个节点我们可以访问图中任何其他节点的图称为连通图。
6. 断开图 #
从某个节点至少无法到达一个节点的图称为断开图。
7.正则图 #
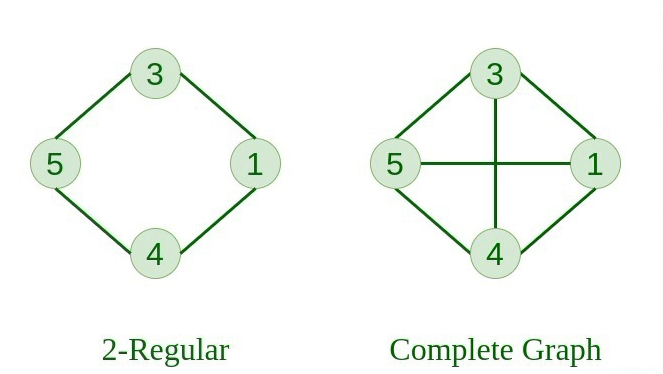
如果图 G 的所有顶点的度数相等,则称简单图是正则图。所有完整的图都是规则的,但反之亦然是不可能的。正则图是一种无向图,其中每个顶点都具有相同数量的边或邻居。换句话说,如果图是正则图,则每个顶点都具有相同的度。
8. 完整图表 #
该图中每个节点都有一条到其他节点的边。
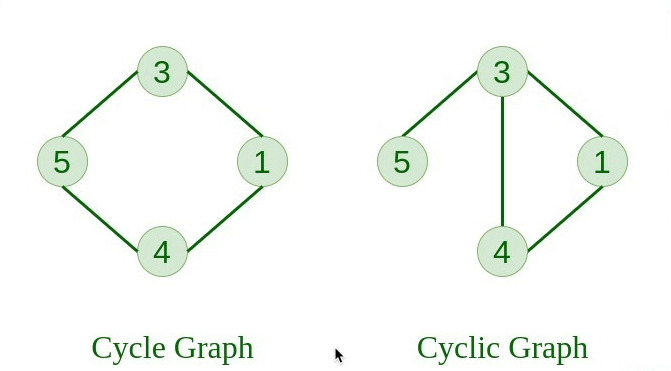
9. 循环图 #
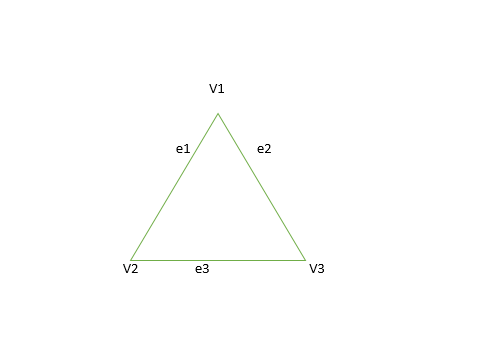
该图本身是一个环,由 n 个顶点组成的图 G,且 n> = 3 即 V1, V2, V3- – – – Vn 和边 (V1, V2), (V2, V3), (V3, V4)- – – – (Vn, V1) 称为循环图。
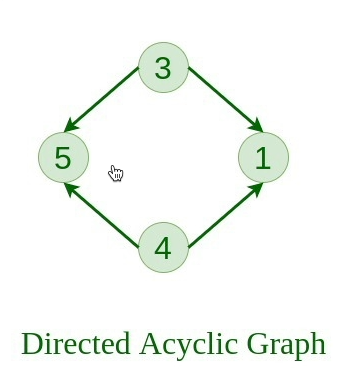
10. 有向无环图 #
不包含任何循环的有向图。
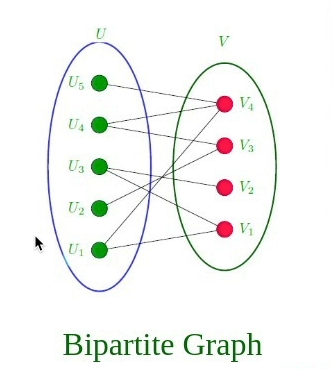
11.二分图 #
一种图,其中的顶点可以分为两个集合,每个集合中的顶点之间不包含任何边。
12. 加权图
- 边已指定适当权重的图称为加权图。
- 带权图又可以分为有向带权图和无向带权图。
13. 跨越子图
考虑如下所示的图 G(V,E)。生成子图是包含原始图 G 的所有顶点的子图,如果 V’=V 并且 E’ 是 E 的子集,则 G’(V’,E’) 是生成的。
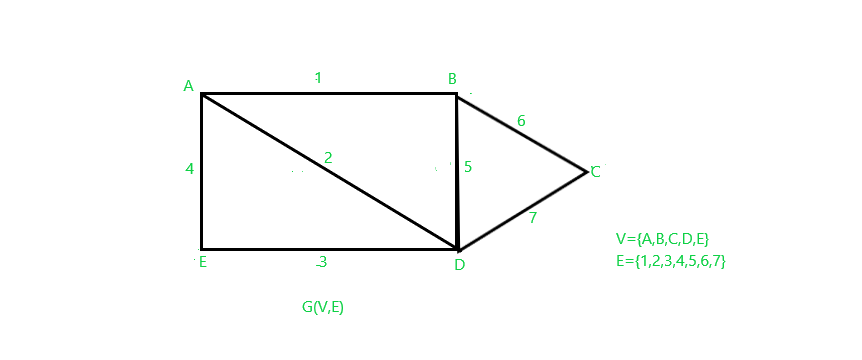
因此,其中一个生成子图可以如下所示 G’(V’,E’)。它具有原始图G的所有顶点和G的一些边。
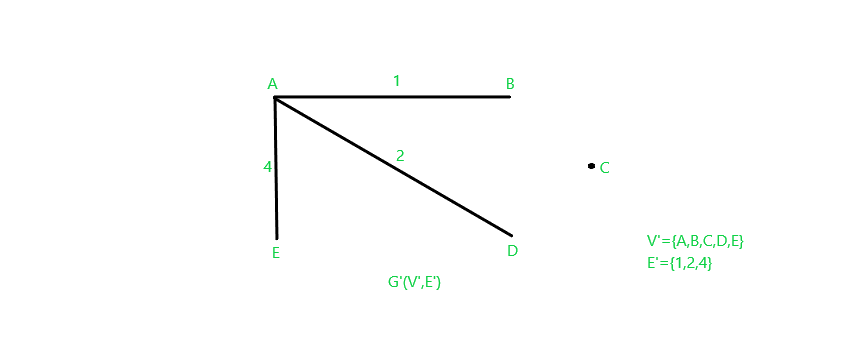
这只是图 G 的众多跨越子图之一。我们可以通过不同的边组合创建各种其他跨越子图。请注意,如果我们考虑图 G’(V’,E’),其中 V’=V 且 E’=E,则图 G’ 是图 G(V,E) 的生成子图。
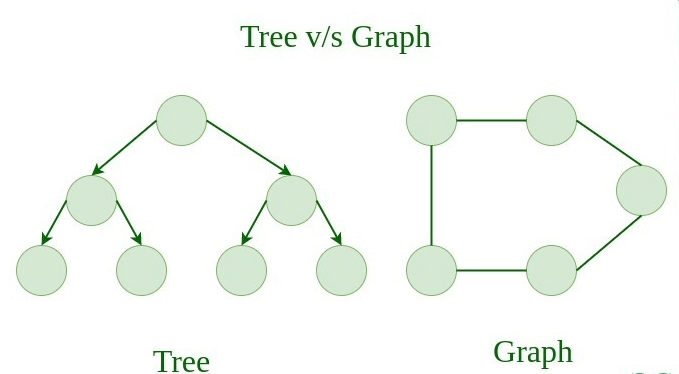
树与图 #
树是受限制的图类型,只是有更多的规则。每棵树总是一个图,但并非所有图都是树。链表、树和堆都是图的特殊情况。
图的表示 #
存储图表有两种方法:
- 邻接矩阵
- 邻接表
邻接矩阵 #
邻接矩阵是将图表示为布尔值(0 和 1)矩阵的一种方式。在此方法中,图以二维矩阵的形式存储,其中行和列表示顶点。矩阵中的每个条目表示这些顶点之间的边的权重。
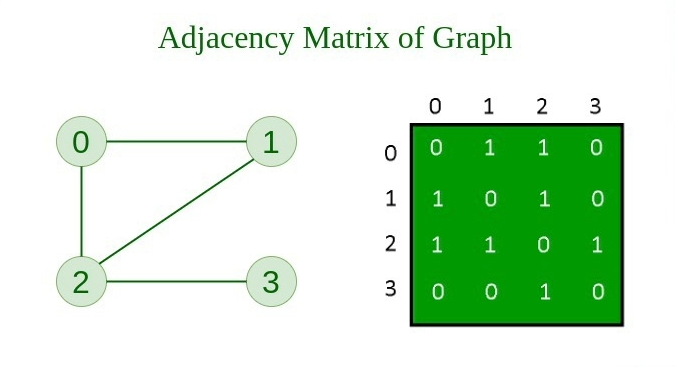
- 如果存在从顶点 i 到 j 的边,则将
adjMat[i][j]标记为1。 - 如果从顶点 i 到 j 没有边,则将
adjMat[i][j]标记为 0。
无向图到邻接矩阵的表示: #
下图显示了一个无向图。最初,整个 Matrix 初始化为 0。如果从源到目标有一条边,我们会在两种情况下插入1 (adjMat[destination]和 adjMat[ destination]),因为我们可以选择任何一种方式。
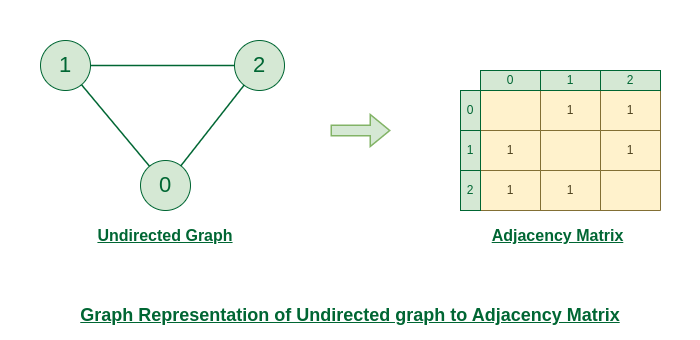
无向图到邻接矩阵
有向图到邻接矩阵的表示: #
下图显示了一个有向图。最初,整个 Matrix 初始化为0。如果从源到目标有一条边,我们为该特定的adjMat[destination]插入1。
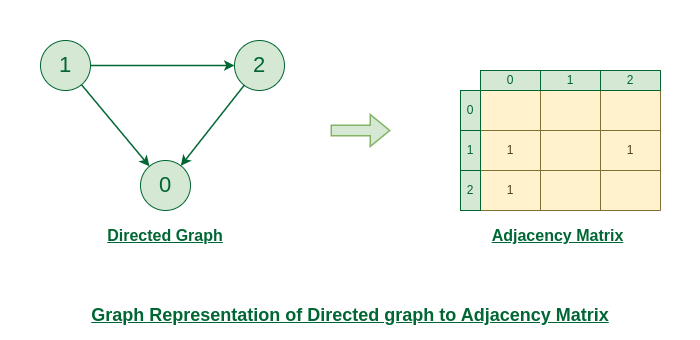
有向图到邻接矩阵
邻接表 #
该图表示为链表的集合。有一个指针数组,它指向连接到该顶点的边。
列表数组用于存储两个顶点之间的边。数组的大小等于顶点的数量(即n)。该数组中的每个索引代表图中的一个特定顶点。数组索引 i 处的条目包含一个链表,其中包含与顶点i相邻的顶点。
假设图中有n 个顶点,因此,创建一个大小为n的列表数组作为adjList[n]。
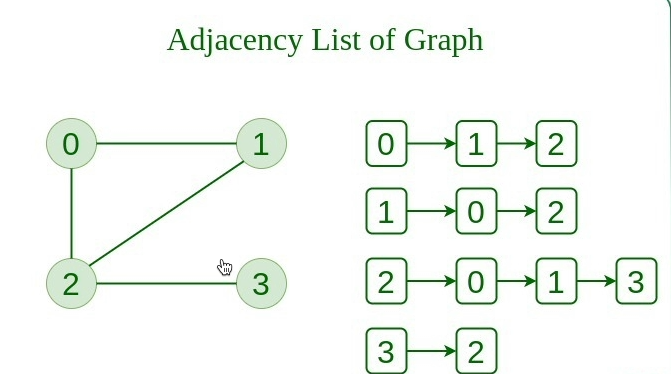
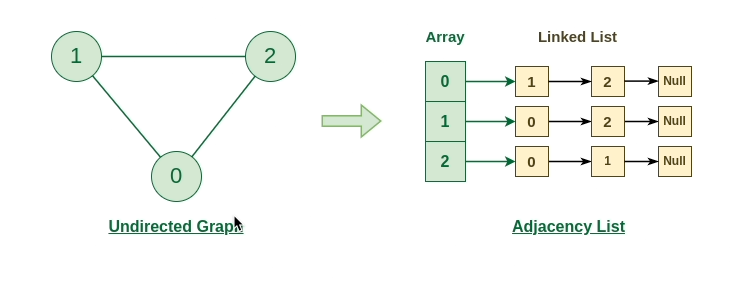
无向图到邻接表的表示: #
下面的无向图有 3 个顶点。因此,将创建一个大小为 3 的列表数组,其中每个索引代表顶点。现在,顶点 0 有两个邻居(即 1 和 2)。因此,在数组的索引 0 处插入顶点 1 和 2。类似地,对于顶点 1,它有两个邻居(即 2 和 1),因此,在数组的索引 1 处插入顶点 2 和 1。类似地,对于顶点 2,将其邻居插入列表数组中。
邻接矩阵与邻接表的比较 #
当图包含大量边时,最好将其存储为矩阵,因为矩阵中只有一些条目为空。 使用Prim和 Dijkstra邻接矩阵等算法可以降低复杂度。
| 行动 | 邻接矩阵 | 邻接表 |
|---|---|---|
| 添加边缘 | 复杂度(1) | 复杂度(1) |
| 移除边缘 | 复杂度(1) | 在) |
| 正在初始化 | O(N*N) | 在) |
图的基本操作 #
以下是图表上的基本操作:
- 在图中插入节点/边 – 将节点插入到图中。
- 删除图中的节点/边 – 从图中删除节点。
- 在图表上搜索 – 在图表中搜索实体。
- 图的遍历——遍历图中的所有节点。
图表的使用 #
- 地图可以用图形来表示,然后可以被计算机用来提供各种服务,例如两个城市之间的最短路径。
- 当各种任务相互依赖时,这种情况可以使用有向无环图来表示,并且我们可以使用拓扑排序找到可以执行任务的顺序。
- 状态转换图表示当前状态的合法移动。在井字游戏中可以使用此功能。
图的实际应用 #
以下是现实生活中的应用: #
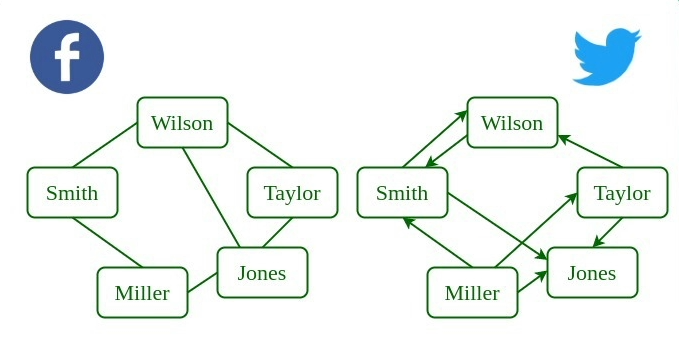
- 图数据结构可用于表示团队中球员之间的交互,例如传球、射门和铲球。分析这些交互可以深入了解团队动态和需要改进的领域。
- 通常用于表示社交网络,例如社交媒体上的朋友网络。
- 图可以用来表示计算机网络的拓扑结构,例如路由器和交换机之间的连接。
- 图表用于表示交通网络中不同地点(例如道路和机场)之间的连接。
- **神经网络:**顶点代表神经元,边代表神经元之间的突触。神经网络用于了解我们的大脑如何工作以及学习时连接如何变化。人脑约有 10^11 个神经元和接近 10^15 个突触。
- **编译器:**图在编译器中广泛使用。它们可用于类型推断、所谓的数据流分析、寄存器分配和许多其他目的。它们还用于专门的编译器,例如数据库语言中的查询优化。
- **机器人规划:**顶点表示机器人可能处于的状态,边表示状态之间可能的转换。例如,此类图形计划可用于规划自动驾驶车辆的路径。
何时使用图表: #
- 当您需要表示和分析不同对象或实体之间的关系时。
- 当您需要执行网络分析时。
- 当您需要识别系统中的关键参与者、影响者或瓶颈时。
- 当您需要做出预测或建议时。
- 网络建模:图通常用于对各种类型的网络进行建模,例如社交网络、交通网络和计算机网络。在这些情况下,顶点代表网络中的节点,边代表它们之间的连接。
- 查找路径:图通常用于查找图中两个顶点之间的路径的算法,例如最短路径算法。例如,图表可用于在地图上查找两个城市之间的最快路线或在多个目的地之间旅行的最有效方式。
- 表示数据关系:图可用于表示数据对象之间的关系,例如数据库或数据结构中的关系。在这些情况下,顶点代表数据对象,边代表它们之间的关系。
- 分析数据:图可用于分析和可视化复杂数据,例如数据聚类算法或机器学习模型。在这些情况下,顶点代表数据点,边代表它们之间的相似点或差异。
然而,在某些情况下,使用图表可能不是最好的方法。例如,如果所表示的数据非常简单或结构化,则图表可能有点过分,更简单的数据结构可能就足够了。此外,如果图非常大或复杂,则分析或遍历可能会很困难或计算成本很高,这可能会使使用图变得不太理想。
图的优点和缺点: #
优点: #
- 图是一种通用的数据结构,可用于表示各种关系和数据结构。
- 它们可用于建模和解决各种问题,包括寻路、数据聚类、网络分析和机器学习。
- 图算法通常非常高效,可以用来快速有效地解决复杂问题。
- 图可以用简单直观的方式表示复杂的数据结构,使其更易于理解和分析。
缺点: #
- 图可能很复杂且难以理解,特别是对于不熟悉图论或相关算法的人来说。
- 创建和操作图的计算成本可能很高,尤其是对于非常大或复杂的图。
- 图算法可能很难正确设计和实现,并且很容易出现错误。
- 图表可能难以可视化和分析,尤其是对于非常大或复杂的图表,这使得从数据中提取有意义的见解变得困难。
概括: #
- 图数据结构是表示和分析对象或实体之间关系的强大工具。
- 图表可用于表示不同对象或实体之间的交互,然后分析这些交互以识别模式、集群、社区、关键参与者、影响者、瓶颈和异常。
- 在体育数据科学中,图数据结构可用于分析和理解球队表现和场上球员互动的动态。
- 它们可用于体育、社交媒体、交通、网络安全等各个领域。
