↓跳过正文
  1. 数据结构与算法/

·1046 字·5 分钟· loading
demo007x
作者
demo007x
目录

如何使用 Dijkstra 算法找到从源到所有顶点的最短路径
#

给定一个图和图中的源顶点，找到从源到给定图中所有顶点的最短路径。

例子：
#

输入： src = 0，图形如下图所示。

img

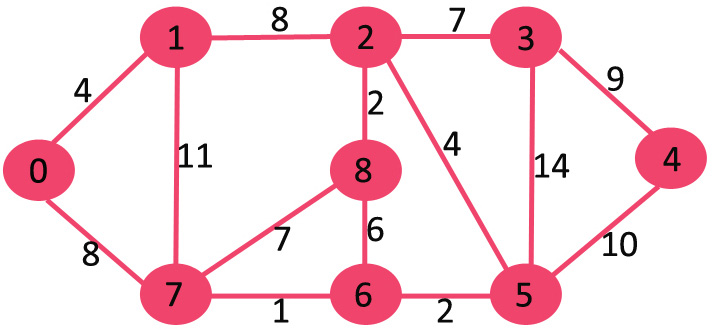
输出： 0 4 12 19 21 11 9 8 14 解释：

从 0 到 1 的距离 = 4 从 0 到 2 的最小距离 = 12 0->1->2 从 0 到 3 的最小距离 = 19 0 ->1->2->3 从 0 到 4 的最小距离 = 21 0->7->6->5->4 从 0 到 5 的最小距离 = 11 0->7->6- >5 从 0 到 6 的最小距离 = 9 0->7->6 从 0 到 7 的最小距离 = 8 0->7 从 0 到 8 的最小距离 = 14 0->1->2 ->8

O(V 2 )中邻接矩阵的 Dijkstra 最短路径算法：
#

这个想法是生成一个以给定源作为根的*SPT（最短路径树） 。*维护具有两组的邻接矩阵，

  • 一组包含最短路径树中包含的顶点，
  • 其他集合包括尚未包含在最短路径树中的顶点。

在算法的每一步中，找到另一个集合（尚未包含的集合）中的一个顶点，并且与源的距离最小。

按照以下步骤解决问题：
#

  • 创建一个集合sptSet（最短路径树集），用于跟踪最短路径树中包含的顶点，即计算并最终确定其到源的最小距离。最初，该集合是空的。
  • 为输入图中的所有顶点分配距离值。将所有距离值初始化为INFINITE。将源顶点的距离值指定为 0，以便首先拾取它。
  • 虽然 sptSet 不包含所有顶点
    • 选择sptSet中不存在且具有最小距离值的 顶点u 。
    • 将 u 包含到sptSet中。
    • 然后更新 u 的所有相邻顶点的距离值。
      • 要更新距离值，请迭代所有相邻顶点。
      • 对于每个相邻顶点 v，如果 u（距源）的距离值与边 uv 的权重之和小于 v 的距离值，则更新 v 的距离值。

**注意：**我们使用布尔数组 sptSet[] 来表示 SPT 中包含的顶点集。如果值 sptSet[v] 为 true，则顶点 v 包含在 SPT 中，否则不包含在 SPT 中。数组dist[]用于存储所有顶点的最短距离值。

下面是上述方法的图示：

插图：

为了理解 Dijkstra 算法，让我们看一张图并找到从源到所有节点的最短路径。

考虑下图并且src = 0

img

步骤1：
#

  • 集合sptSet最初为空，分配给顶点的距离为 {0, INF, INF, INF, INF, INF, INF, INF}，其中INF表示无限。
  • 现在选择具有最小距离值的顶点。选取顶点 0，将其包含在sptSet中。因此sptSet变为 {0}。将 0 包含到sptSet后，更新其相邻顶点的距离值。
  • 0 的相邻顶点是 1 和 7。1 和 7 的距离值更新为 4 和 8。

下面的子图显示了顶点及其距离值，仅显示了具有有限距离值的顶点。SPT 中包含的顶点以绿色显示。

img

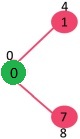
第2步：
#

  • 选择具有最小距离值且尚未包含在 SPT 中（不在 sptSET 中）的顶点。顶点 1 被选取并添加到 sptSet 中。
  • 因此 sptSet 现在变为 {0, 1}。更新相邻顶点的距离值为1。
  • 顶点2的距离值变为12。

img

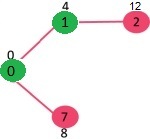
步骤3：
#

  • 选择具有最小距离值且尚未包含在 SPT 中（不在 sptSET 中）的顶点。选择顶点 7。因此 sptSet 现在变为**{0, 1, 7}。**
  • 更新 7 的相邻顶点的距离值。顶点 6 和 8 的距离值变为有限（分别为15 和 9）。

img

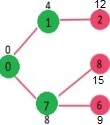
步骤4：
#

  • 选择具有最小距离值且尚未包含在 SPT 中（不在 sptSET 中）的顶点。选择顶点 6。所以 sptSet 现在变成了**{0, 1, 7, 6}**。
  • 更新6的相邻顶点的距离值。更新顶点5和8的距离值。

img

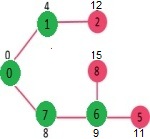
我们重复上述步骤，直到sptSet包含给定图的所有顶点。最后，我们得到如下的最短路径树（SPT）。

img

下面是上述方法的实现：
#

  • Javascript
// 用于Dijkstra单源最短路径算法的Javascript程序。
// 该程序适用于图的邻接矩阵表示。
let V = 9;

// 用于找到具有最小距离值的顶点的实用函数，该顶点来自尚未包含在最短路径树中的顶点集合
function minDistance(dist, sptSet) {
  // 初始化最小值
  let min = Number.MAX_VALUE;
  let min_index = -1;

  for (let v = 0; v < V; v++) {
    if (sptSet[v] == false && dist[v] <= min) {
      min = dist[v];
      min_index = v;
    }
  }
  return min_index;
}

// 用于打印构建的距离数组的实用函数
function printSolution(dist) {
  console.log("Vertex \t\t Distance from Source\n\r");
  for (let i = 0; i < V; i++) {
    console.log(i + " \t\t " + dist[i] + "\n\r");
  }
}

// 实现Dijkstra算法的函数
// 用邻接矩阵表示的图的单源最短路径算法
function dijkstra(graph, src) {
  let dist = new Array(V);
  let sptSet = new Array(V);

  // 将所有距离初始化为无穷大，并将stpSet[]设置为false
  for (let i = 0; i < V; i++) {
    dist[i] = Number.MAX_VALUE;
    sptSet[i] = false;
  }

  // 源顶点到自身的距离始终为0
  dist[src] = 0;

  // 查找所有顶点的最短路径
  for (let count = 0; count < V - 1; count++) {
    // 从尚未处理的顶点集中选择最小距离的顶点
    // 在第一次迭代中，u始终等于src。
    let u = minDistance(dist, sptSet);

    // 将选择的顶点标记为已处理
    sptSet[u] = true;

    // 更新选定顶点的相邻顶点的距离值。
    for (let v = 0; v < V; v++) {
      // 仅在v不在sptSet中、从u到v存在边，并且通过u从src到v的路径的总权重小于dist[v]当前值时，更新dist[v]'
      if (
        !sptSet[v] &&
        graph[u][v] != 0 &&
        dist[u] != Number.MAX_VALUE &&
        dist[u] + graph[u][v] < dist[v]
      ) {
        dist[v] = dist[u] + graph[u][v];
      }
    }
  }

  printSolution(dist);
}

let graph = [
  [0, 4, 0, 0, 0, 0, 0, 8, 0],
  [4, 0, 8, 0, 0, 0, 0, 11, 0],
  [0, 8, 0, 7, 0, 4, 0, 0, 2],
  [0, 0, 7, 0, 9, 14, 0, 0, 0],
  [0, 0, 0, 9, 0, 10, 0, 0, 0],
  [0, 0, 4, 14, 10, 0, 2, 0, 0],
  [0, 0, 0, 0, 0, 2, 0, 1, 6],
  [8, 11, 0, 0, 0, 0, 1, 0, 7],
  [0, 0, 2, 0, 0, 0, 6, 7, 0],
];
dijkstra(graph, 0);

输出

距源的顶点距离
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
  • Python 代码:
# Dijkstra的单源最短路径算法的Python程序。
# 该程序用于图的邻接矩阵表示。
  import sys
  class Graph():
  
  	def __init__(self, vertices):
  		self.V = vertices
  		self.graph = [[0 for column in range(vertices)]
  					for row in range(vertices)]
  
  	def printSolution(self, dist):
  		print("顶点距离源的距离")
  		for node in range(self.V):
  			print(node, "\t", dist[node])
  
  	# 一个实用函数，用于从尚未包含在最短路径树中的顶点集中找到具有最小距离值的顶点
  	def minDistance(self, dist, sptSet):
  
  		# 初始化下一个节点的最小距离
  		min = sys.maxsize
  		＃ 搜索不是最近的顶点，也不在最短路径树中
  		for u in range(self.V):
  			if dist[u] < min and sptSet[u] == False:
  				min = dist[u]
  				min_index = u
  
  		return min_index
  
  	# 实现Dijkstra单源最短路径算法的函数
		# 使用邻接矩阵表示的图形来表示
  	def dijkstra(self, src):
  
  		dist = [sys.maxsize] * self.V
  		dist[src] = 0
  		sptSet = [False] * self.V
  
  		for cout in range(self.V):
  
  			# 从尚未处理的顶点集中选择最小距离的顶点。
				# 在第一次迭代中，x始终等于src。
  			x = self.minDistance(dist, sptSet)
  
  		# 将最小距离顶点放入
			# 最短路径树
  			sptSet[x] = True
  
  			# 更新相邻顶点的距离值
				# 只有当当前距离大于新距离时，才更新选取顶点的
				# 距离大于新距离，且该顶点不在最短路径树中
  			for y in range(self.V):
  				if self.graph[x][y] > 0 and sptSet[y] == False and \
  						dist[y] > dist[x] + self.graph[x][y]:
  					dist[y] = dist[x] + self.graph[x][y]
  
  		self.printSolution(dist)
  
  if __name__ == "__main__":
  	g = Graph(9)
  	g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
  			[4, 0, 8, 0, 0, 0, 0, 11, 0],
  			[0, 8, 0, 7, 0, 4, 0, 0, 2],
  			[0, 0, 7, 0, 9, 14, 0, 0, 0],
  			[0, 0, 0, 9, 0, 10, 0, 0, 0],
  			[0, 0, 4, 14, 10, 0, 2, 0, 0],
  			[0, 0, 0, 0, 0, 2, 0, 1, 6],
  			[8, 11, 0, 0, 0, 0, 1, 0, 7],
  			[0, 0, 2, 0, 0, 0, 6, 7, 0]
  			]
  
  	g.dijkstra(0)

时间复杂度： O(V 2 ) 辅助空间： O(V)

笔记：

  • 该代码计算最短距离，但不计算路径信息。创建一个父数组，当距离更新时更新父数组，并用它来显示从源到不同顶点的最短路径。
  • 该代码适用于无向图，相同的 Dijkstra 函数也可用于有向图。
  • 该代码查找从源到所有顶点的最短距离。如果我们只对从源到单个目标的最短距离感兴趣，则当选取的最小距离顶点等于目标时，将它们打断循环。
  • 实现的时间复杂度是O(V 2 )。如果输入 图使用邻接表表示，则可以借助二叉堆将其简化为 O(E * log V)。
  • Dijkstra 算法不适用于具有负权循环的图。对于具有负边的图，它可能会给出正确的结果，但您必须允许一个顶点可以被多次访问，并且该版本将失去其快速时间复杂度。

Dijkstra 使用 O(E logV) 中的堆实现邻接表的最短路径算法：
#

对于Dijkstra算法，始终建议使用 堆（或优先级队列），因为所需的操作（提取最小值和减少键）与堆（或优先级队列）的特性相匹配。然而，问题是，priority_queue 不支持减键。要解决此问题，请不要更新密钥，而是再插入一个密钥副本。因此，我们允许优先级队列中存在同一顶点的多个实例。这种方法不需要减少关键操作，并且具有以下重要属性。

  • 每当一个顶点的距离减少时，我们就会在priority_queue中添加一个顶点实例。即使有多个实例，我们也只考虑距离最小的实例，而忽略其他实例。
  • 时间复杂度仍然是O(E * LogV)，因为优先级队列中最多有 O(E) 个顶点，并且 O(logE) 与 O(logV) 相同

下面是上述方法的实现：

  • Javascript

    <script>
// 使用STL中的优先队列来找到Dijkstra最短路径的JavaScript程序
const INF = 2147483647;

// 这个类使用邻接表表示有向图
class Graph {

	constructor(V){

		// 节点数量
		this.V = V;

		// 在一个带权图中，我们需要为每条边存储顶点和权重对
		this.adj = new Array(V);
		for(let i = 0; i < V; i++){
			this.adj[i] = new Array();
		}
	}

	addEdge(u, v, w)
	{
		this.adj[u].push([v, w]);
		this.adj[v].push([u, w]);
	}

	// 从源节点打印到所有其他顶点的最短路径
	shortestPath(src)
	{
		// 创建一个优先队列来存储正在预处理的顶点。这是C++中的奇怪语法。
		// 请参考下面链接了解此语法的详细信息
		let pq = [];

		// 创建一个距离向量并将所有距离初始化为无穷大（INF）
		let dist = new Array(V).fill(INF);

		// 将源本身插入优先队列并将其距离初始化为0。
		pq.push([0, src]);
		dist[src] = 0;

		// 循环直到优先队列为空（或所有距离未被最终确定）。
		while (pq.length > 0) {
			// 第一个顶点对中的第一个顶点是最小距离的顶点，从优先队列中提取它。
			// 顶点标签存储在第二个元素中（必须以这种方式完成以保持顶点按距离排序（距离必须是对中的第一项））。
			let u = pq[0][1];
			pq.shift();

			// 'i' 用于获取一个顶点的所有相邻顶点。
			for(let i = 0; i < this.adj[u].length; i++){
				// 获取当前u的相邻顶点的标签和权重。
				let v = this.adj[u][i][0];
				let weight = this.adj[u][i][1];

				// 如果通过u存在到v的更短路径。
				if (dist[v] > dist[u] + weight) {
					// Updating distance of v
					dist[v] = dist[u] + weight;
					pq.push([dist[v], v]);
					pq.sort((a, b) =>{
						if(a[0] == b[0]) return a[1] - b[1];
						return a[0] - b[0];
					});
				}
			}
		}

		// 打印存储在dist[]中的最短距离
		document.write("Vertex Distance from Source");
		for (let i = 0; i < V; ++i)
			document.write(i, "	 ", dist[i]);
	}
}

let V = 9;
let g = new Graph(V);

// 制作上面显示的图表
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);

g.shortestPath(0);

</script>

时间复杂度： O(E * logV)，其中E是边数，V是顶点数。 辅助空间： O(V)

相关文章

如何编写正则表达式？
Notes 正则表达式 Tools
正则表达式 (regex) 是定义搜索模式的字符序列。以下是编写正则表达式的方法：1. 首先了解正则表达式中
使用Docker config 存储数据
docker devops
使用Docker config 存储数据
WebSocket
Notes JavaScript HTTP socket
WebSocket 对象提供了用于创建和管理 [WebSocket]( https://developer.mo