图数据结构与算法应用
#

数学| 图表中的步行、步道、路径、自行车和电路
#

步行是图的一系列顶点和边，即如果我们遍历图，那么我们就得到了步行。边和顶点都可以重复。

这里，1->2->3->4->2->1->3 是步行。

步行可以是开放式的，也可以是封闭式的。

开放步行: 如果起始顶点和结束顶点不同，即起始顶点和终止顶点不同，则称步行为开放步行。 闭合步行: 如果起始和结束顶点相同，即如果步行在同一顶点开始和结束，则称其为闭合步行。

上图中： 1->2->3->4->5->3 是一条开放走道。 1->2->3->4->5->3->1 是封闭的路线。

最优路径是一条开放的路径，其中没有重复的边缘。

顶点可以重复。

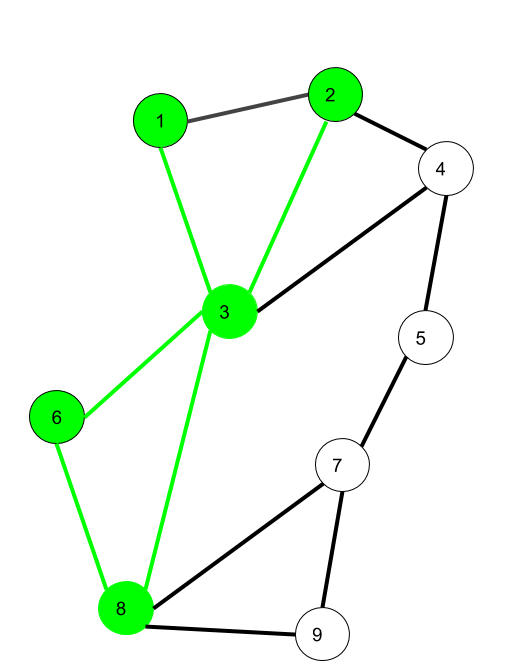
这里 1->3->8->6->3->2 是路径另外 1->3->8->6->3->2->1 是封闭的路线

遍历一个图，使得边不重复，但顶点可以重复，并且它也是闭合的，即它是闭合轨迹。

顶点可以重复。边不能重复。

这里1->2->4->3->6->8->3->1是一个电路。

环路是一条封闭的小路。这些只能有重复的顶点。

它是一条既不重复顶点也不重复边的路径，即如果我们遍历一个图，那么我们不重复顶点也不重复边。由于路径也是一条小路，因此它也是一条开放的步行道。

路径的另一个定义是没有重复顶点的路线。这直接意味着没有边会重复，因此在路径定义中写入是多余的。

顶点不重复，边不重复

这里 6->8->3->1->2->4 是一个路径

遍历一个图，这样我们不重复一个顶点，也不重复一条边，但起始和结束顶点必须相同，即只有当我们得到一个循环时，我们才能重复起始和结束顶点。

顶点不重复 ,边不重复

这里1->2->4->3->1是一个循环。

循环是一条闭合路径。这些不能重复任何东西（边或顶点都不能）。

请注意，对于闭合序列，起始顶点和结束顶点是唯一可以重复的顶点。